Математика 4 класс учебник Петерсон 1 часть ответы – страница 4

Подставим в неравенства данные числа вместо неизвестного и узнаем являются ли они решениями неравенства.
а) 8 · b – 7 > 90,
при b = 6, получим8 · 6 – 7 > 9048 – 7 > 9041 > 90 – не верно.Значит, число 6 не будет решением неравенства.
при b = 9, получим8 · 9 – 7 > 9072 – 7 > 9065 > 90 – не верно.Значит, число 9 не будет решением неравенства.
при b = 12, получим8 · 12 – 7 > 9096 – 7 > 9089 > 90 – не верно.Значит, число 12 не будет решением неравенства.
при b = 30, получим8 · 30 – 7 > 90240 – 7 > 90233 > 90 – верно.Значит, число 30 будет решением неравенства.
при b = 72, получим8 · 72 – 7 > 90

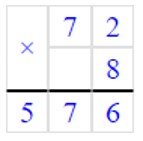
576 − 7 > 90569 > 90 – верно.Значит, число 72 будет решением неравенства.

б) d : 3 + 9 < 12,
при d = 6, получим6 : 3 + 9 < 122 + 9 < 1211 < 12 – верно.Значит, число 6 будет решением неравенства.
при d = 9, получим9 : 3 + 9 < 123 + 9 < 1212 < 12 – не верно.Значит, число 9 не будет решением неравенства.
при d = 12, получим12 : 3 + 9 < 124 + 9 < 1213 < 12 – не верно.Значит, число 12 не будет решением неравенства.
при d = 30, получим30 : 3 + 9 < 1210 + 9 < 1219 < 12 – не верно.Значит, число 30 не будет решением неравенства.
при d = 72, получим72 : 3 + 9 < 12

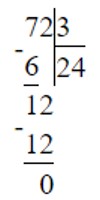
24 + 9 < 1233 < 12 – не верно.Значит, число 72 не будет решением неравенства.
Ответ: а) 30 и 72; б) 6.

а) n – 3 > 960    n > 960 + 3    n > 963    n – может быть любым числом, которое больше 963.    Пример: n = 1000, n = 1001.
б) 43 · m < 100    m < 100 : 43

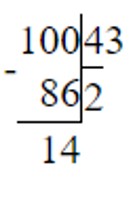
    m < 2 (ост. 14)    m – может быть любым числом, которое меньше или равным 2.    Пример: m = 1, m = 2.
в) 180 : y > 20    y < 180 : 20    y < 9    y – может быть любым числом, которое меньше 9 и не равное 0 (Так как на 0 делить нельзя).    Пример: y = 1, y = 3.

а) 7 · c < 9    c < 9 : 7    c < 1 (ост. 2)    Неравенство верно при c равном 0 или 1.
б) 12 : d > 3    d < 12 : 3    d < 4    Неравенство верно при d равном 1, 2 или 3.
в) x · 7 < 21    x < 21 : 7    x < 3    Неравенство верно при x равном 0, 1 или 2.
г) y · 5 < 1    y < 1 : 5    y < 0 (ост. 1)    Неравенство верно при y = 0.
д) b + b < 4    2 · b < 4    b < 4 : 2    b < 2    Неравенство верно при b равном 0 или 1.
е) 3 – t > 2    t < 3 – 2    t < 1    Неравенство верно при t = 0.

1) 14 : 2 = 7 (км/ч) – скорость зайца;2) 210 : 3 = 70 (км/ч) – скорость сокола;3) 70 : 7 = 10 (раз) – во сколько раз сокол движется быстрее, чем заяц;4) 70 – 7 = 63 (км/ч) – на сколько километров в час скорость зайца меньше скорости сокола.
Заполним таблицу:

Решение:1) 14 – 6 = 8 (км) – прошли до привала2) 14 + 8 = 22 (км) – прошли всего3) 22 · 3 = 66 (км) – сколько осталось пройти4) 22 + 66 = 88 (км) – весь путьОтвет: 88 км.

а) (786 – 600) · 19 + (1007 – 965) · 14 – 48 · 16 = 3354
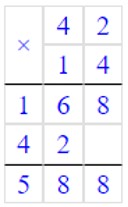
1) 786 – 600 = 1862) 1007 – 965 = 423) 186 · 19 - 3534

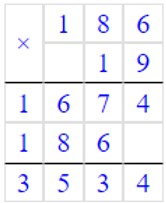
4) 42 · 14 = 588

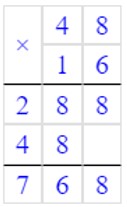
5) 48 · 16 = 768

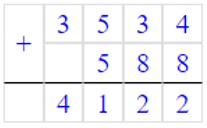
6) 3534 + 588 = 4122

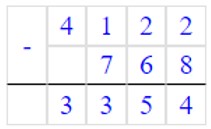
7) 4122 – 768 = 3354

б) (9867 + 76535) · 105 – 96 + 78 · (1080 – 789) = 9094812
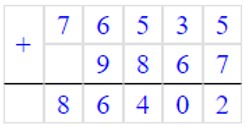
1) 9867 + 76535 = 86402

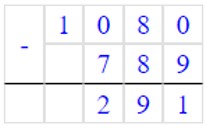
2) 1080 – 789 = 291

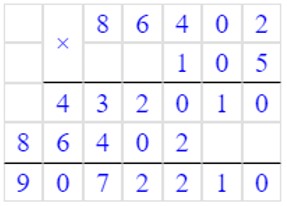
3) 86402 · 105 = 9072210

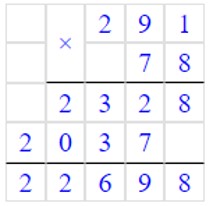
4) 78 · 291 = 22698

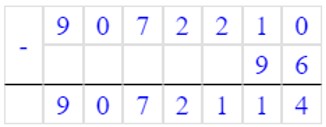
5) 9072210 – 96 = 9072114

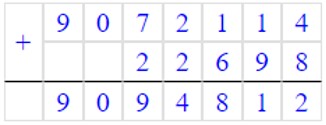
6) 9072114 + 22698 = 9094812

Числа в нижней строке – это количество дней в месяцах, так как в январе – 31 день, в феврале – 28 или 29. Тогда числа в верхней строке – это количество букв в названиях месяцев.
Январь – 6 букв и 31 день;Февраль – 7 букв и 28 или 29 дней;Март – 4 буквы и 31 день;Апрель – 6 букв и 30 дней;Май – 3 буквы и 31 день;Июнь – 4 буквы и 30 дней;Июль – 4 буквы и 31 день;Август – 6 букв и 31 день;Сентябрь – 8 букв и 30 дней.
Заполним таблицу: